Vertical Fog及在Fragment Shader中重建世界坐标

并不是那么简单的坐标重建问题

作者 Jingping Yu 日期 2016-12-04
Unity Computer Graphics Shader

本文同时也发表在我的知乎专栏上😄.

作者：音速键盘猫

链接：https://zhuanlan.zhihu.com/p/24160707?refer=MeowShader

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Vertical Fog (垂直雾) 是什么

想必大家都知道雾特效, 一般来讲, 距离摄像机越远的点, 其受到雾特效的影响会越为严重. 这是最为常见的雾特效.

但是还有一种雾, 在某一点的浓度与其和观察点间的距离关系似乎并不大, 而与其世界位置坐标有非常紧密的联系.

我不太懂物理, 姑且理解为雾霾因自身受到的重力而产生了沉积作用, 使得距离地面较近的区域雾浓度特别高, 但是一旦高过某个阈值, 浓度则开始急剧下降.

以上属于我的不懂装懂辣鸡解释. 如果某位大侠能够科学地解释一下, 感激不尽.

以上三张照片全部来自谷歌图片, 摄于Dubai.

知道了Vertical Fog是什么东西之后, 我们就需要知道这个特效有什么用.

在很多Top-Down类型的游戏(比如LOL, Dota, Space Marshall)中想要加入雾特效的话, 使用传统的基于距离和深度的雾特效会导致效果失真. 这是因为Top-Down的视角是比较广的, 简单粗暴地糊上一层雾会导致许多距离摄像机较远, 但又很重要的部分被渲染为白茫茫的雾. 与此相反, 我们只希望在放置GameObject的那一层产生比较集中的雾, 因此可以考虑基于每一个点的世界坐标决定其雾的浓度.

本文将要实现基于Image Effect的Vertical Fog效果. 当然了思路是相通的, 如果想要局部地添加雾特效, 也可以将类似的着色器特效应用于模型上, 然后注意调整模型的Blend与ZTest就好了.

猜一猜这个特效要怎么实现

恩, 假设我们什么都不知道, 只有一个处理前的图和处理后的效果图:

原图

处理后

通过上面的两张图, 我们能得到如下的结论:

  • 1 某点的雾的浓度, 和该点的世界Y坐标有关系.
  • 2 某点的雾的浓度, 和摄像机的位置, FOV, 角度等都没有任何关系.
  • 3 雾的浓度符合某种数学公式, 使其沉积在了比较低的区域.
  • 4 这个特效适合俯视被观察区域的情况. 如果身在雾中的话, 恐怕什么都看不清楚.

很明显, 只要能知道某一点的世界Y坐标, 那什么问题都解决了.

一个Naive的思路 (直白而低效)

在片元着色器中逆推出每一个片元的View Space坐标, 然后乘以_InverseView矩阵将之转化回World Space.

首先我们将片元屏幕坐标重新映射到[-1, 1]的区间以回归到NDC Space, 随后将NDC Space转化为View Space, 再通过从C#脚本传入的摄像机的世界-摄像机变换矩阵的逆求出其世界坐标.😏

float depth = LinearEyeDepth ( SAMPLE_DEPTH_TEXTURE( _CameraDepthTexture, i.uv ) ); 
float2 p11_22 = float2 ( unity_CameraProjection._11, unity_CameraProjection._22 ); 
float3 vpos = float3( ( i.uv * 2 - 1) / p11_22, -1 ) * depth; 
float4 wpos = mul( _InverseView, float4( vpos, 1 ) ); 
return wpos.y / 10;//下文中会说到为什么写得这么奇怪.

这段程序中vpos的计算过程为了让代码看起来简单点而做了一点变化, 更加直观的方式是这样的:

float2 ndc = i.uv * 2 - 1;
float3 vpos;
vpos.x = ndc / p11_22.x * depth;
vpos.y = ndc / p11_22.y * depth;
vpos.z = -depth;

unity_CameraProjection中存储的是投影矩阵. (这个是OpenGL的版本)其形式如下:

$$\begin{pmatrix} \frac {2n} {r - l} & 0 & \frac {r + l} {r - l} & 0 \\ 0 & \frac {2n} {t - b} & \frac {t + b} {t - b} & 0 \\ 0 & 0 & \frac {-(f + n)} {f - n} & \frac {-2fn} {f - n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix}$$

点元着色器的坐标变化处理过程如下:

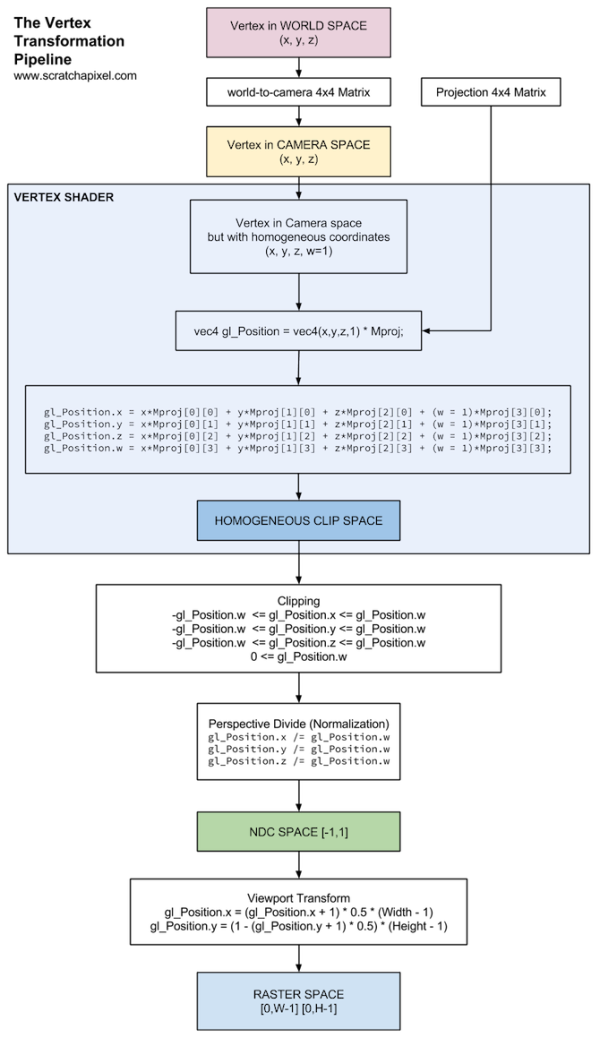
(这个图是DirectX的版本, 换到OpenGL的话, 倒数第二个框框中y的处理应该和x一样)

我们现在相当于在倒数第二个框框内, 唯一不同的是我们采用的是uv坐标, 范围是[0, 1]而并非[0, width]与[0, height]. 因此第二段程序所做的, 就是利用uv坐标来求出NDC Space坐标. 注意, 到此为止完全和Z没有任何关系. 所以我们只需要让x分量除以$\frac {2n} {r - l}$, 让y分量除以$\frac {2n} {t - b}$即可.

转化回NDC Space后, 由于我们本质上已经做过了标准化和剪裁, 因此倒数第四个与第五个框框跳过, 我们的逆推过程进入到了蓝色的大框框中. 而根据坐标变换规则, 我们有如下等式:

$$ x^{'} = \frac {nP_{x}} {-P_{z}} $$ $$ y^{'} = \frac {nP_{y}} {-P_{z}} $$ $$ z^{'} = n $$

OpenGL中View Space的Z轴正方向背离View Frustum. 而通过CameraDepthTexture我们得到的值均为正, 因此需要特殊变换一下.

OK, 到此为止我们已经成功将Screen Space丢到了View Space中, 我们只需要在C#脚本中插入如下代码, 就可以将世界-摄像机变换矩阵的逆传入:

material.SetMatrix ( "_InverseView", GetComponent<Camera> ().cameraToWorldMatrix );

然后, 乘以这个矩阵即可:

float4 wpos = mul ( _InverseView, vpos );

现在说明下为什么我们最后要查看的是wpos.y / 10. 其实这个10是我顺手敲上去的😆, 人眼对于暗色的分辨能力高于对明亮颜色的分辨能力, 因此这个过程非常类似于Gamma Correction. 但是为什么我这没有用乘方的形式进行校正呢? 这是因为严格意义上来讲我们输出的是"坐标", 而游戏场景中的坐标可能会比较大, 比如厨房的柜子顶端其y轴坐标就达到了2.5m. 因此不如简单粗暴地除以10, 这样也很容易查看我们最后的结果是否正常😝.

如图所示, 越高的地方越明亮.

但是, 我们不希望Naive

分析

为什么上面介绍的方法不好? 我们都知道矩阵乘法是一个颇为耗资源的一个操作, 哪怕搬到GPU上也一样. 而上面的做法是在片元着色器中做坐标转换, 屏幕分辨率是多少就做了多少次矩阵乘法 ... 😅

方法

不知道读者是不是和我一样有一种感觉: 一个特定的ViewPort Position和一个特定的深度值, 是能够唯一确定一个世界坐标的. 我不会画图 ... 诸位脑补一下哈, 透视投影的过程中, 处在同一条从摄像机射出的射线上的点, 最终会被绘制到同一个位置上. (这也就是深度测试的意义之一 --- 只让最近的那个点被绘制出来). 但是如果我们又同时知道了射线上的某个点到摄像机的距离, 那么这个点就是唯一确定的😠.

那么最后我们要得到的世界坐标就是$ray * depth + _WorldSpaceCameraPos$.

恩, 如果能快速得到这条射线就好了. 其实得到这条射线的方法简单的令人发指😚.

  • 我们可以在C#脚本中计算出摄像机到其View Frustum的远剪裁面的四个角的世界坐标射线.
  • 对于全屏幕的后期特效, 其实就是一个全屏幕的Quad, 四个顶点. 一个顶点对应上述的一个角.
  • 点元着色器输出至片元着色器的过程中自带插值 ... 我们什么都不用做, 就这么华丽丽地得到了想要的射线.

求View Frustum四个角的世界坐标的C#程序:

Matrix4x4 frustumCorners = Matrix4x4.identity; 
float fovWHalf = camFov * 0.5f; 
Vector3 toRight = m_camTrans.right * camNear * Mathf.Tan (fovWHalf * Mathf.Deg2Rad) * camAspect; 
Vector3 toTop = m_camTrans.up * camNear * Mathf.Tan (fovWHalf * Mathf.Deg2Rad); 
Vector3 topLeft = (m_camTrans.forward * camNear - toRight + toTop); 
float camScale = topLeft.magnitude * camFar/camNear; 
topLeft.Normalize(); 
topLeft *= camScale; 
Vector3 topRight = (m_camTrans.forward * camNear + toRight + toTop); 
topRight.Normalize(); 
topRight *= camScale; Vector3 bottomRight = (m_camTrans.forward * camNear + toRight - toTop); 
bottomRight.Normalize(); 
bottomRight *= camScale; 
Vector3 bottomLeft = (m_camTrans.forward * camNear - toRight - toTop);
bottomLeft.Normalize(); bottomLeft *= camScale; 
frustumCorners.SetRow (0, topLeft); 
frustumCorners.SetRow (1, topRight); 
frustumCorners.SetRow (2, bottomRight); 
frustumCorners.SetRow (3, bottomLeft); 
material.SetMatrix ("_FrustumCornersWS", frustumCorners);

现在我们的问题是如何让这个矩阵代表的四个角与Screen Quad的四个角一一对应.

通过观察, 我们得到了如下关系:

uv.x = 0, uv.y = 0 ------ index = 3;

uv.x = 1, uv.y = 0 ------ index = 2;

uv.x = 1, uv.x = 1 ------ index = 1;

uv.x = 0, uv.y = 1 ------ index = 0;

我们需要知道一个函数F(x, y) = index, 使其能符合上述关系. 否则我们在点元着色器中就要使用if来判断x与y的关系, 从而和z一一对应. 摆脱了矩阵乘法, 然后引入了一坨if ... 这波真亏. 容易推知如下关系: $F(x, y) = abs (3 - x - 3 * y)$.

重获新生的点元着色器

v2f vert (appdata_img v) 
{ 
	v2f o; 
	o.vertex = mul(UNITY_MATRIX_MVP, v.vertex); 
	o.uv = v.texcoord.xy; 
	int xx = (int)v.vertex.x; int yy = (int)v.vertex.y; 
	int z = abs (3 - xx - 3 * yy); 
	o.interpolatedRay = _FrustumCornersWS[ z ]; 
	o.interpolatedRay.w = ( v.vertex.z ); return o; 
}

计算雾的浓度

首先我们获取每一个片元的世界坐标. 由于射线射向的是远剪裁面, 因此这里将DepthBuffer Linearize的时候不要转化成EyeSpace ... 应该是01Space.

float depth = Linear01Depth ( SAMPLE_DEPTH_TEXTURE ( _CameraDepthTexture, UnityStereoScreenSpaceUVAdjust ( i.uv, _CameraDepthTexture_ST ) ) ); 
float3 worldPos = ( depth * i.interpolatedRay ).xyz + _WorldSpaceCameraPos;

然后应用一个随着高度指数衰减的密度函数就可以了, 在这里我随便写了一个, 仅供参考啦😸:

return lerp (tex2D (_MainTex, i.uv), _FogColor, saturate(exp(-worldPos.y - _Start) * _Density));

最终效果

FEATURED TAGS
Unity Computer Graphics Shader